• overview

  • Course welcome

  • wrangle

  • Filter
  • Arrange
  • Mutate
  • Wrap up

  • visualize

  • Getting started
  • Geoms
  • Aesthetics
  • Facets

  • summarize

  • Summarize
  • Group by
    • Visualizing summaries

    • plot types

    • Line plots
    • Bar plots
    • Histograms
    • Boxplots

    Group by

    The group_by verb

    In the last lesson, you used the summarize verb to calculate an average either,

    • across all countries (the entire dataset)
    • within a particular country (filtered data)

    In this lesson you'll learn the group_by verb, which opens up a new option for calculating an average:

    • within each country

    The group_by verb

    You use group_by to define groupings of data (blue and green chunks in diagram).

    Then, you would follow it with summarize to convert those groups to a single value (like a mean).

    The summarize verb

    (music_top200
  >> filter(_.country == "Japan")
  >> summarize(avg_duration = _.duration.mean()))

    avg_duration
    0 250.53499

    For example, here you're finding the average track duration in Japan.

    What if we weren't interested just in the average duration for Japan, but for each country in the dataset?

    You could rerun this code and change the country each time, but that's very tedious.

    Summarizing by country

    (music_top200
  >> group_by(_.country)
  >> summarize(avg_duration = _.duration.mean())
)

    country avg_duration
    0 Argentina 212.847855
    1 Australia 204.795300
    2 Austria 184.894870
    ... ... ...
    59 United States 190.827500
    60 Uruguay 210.796985
    61 Viet Nam 217.222830

    62 rows × 2 columns

    Instead, you can use the group_by verb, which tells siuba to summarize within groups instead of summarizing the entire dataset. Notice that this replaces the filter country equals Japan with group_by country.

    group_by(_.country) tells the summarize step that it should perform the summary within each country: within Argentina, then within Australia, and so on through Viet Nam, then combine the results.

    Instead of getting one row overall, you now get one row for each country. There's now a year variable along with the new avg_duration variable.

    Summarizing by continent and position

    (music_top200
  >> group_by(_.continent, _.position)
  >> summarize(
      min_streams = _.streams.min(),
      max_streams = _.streams.max()
  )
)

    continent position min_streams max_streams
    0 Africa 1 94422 94422
    1 Africa 2 74689 74689
    2 Africa 3 67552 67552
    ... ... ... ... ...
    997 Oceania 198 44570 225951
    998 Oceania 199 44364 225492
    999 Oceania 200 44291 225179

    1000 rows × 4 columns

    You can also group by multiple variables.

    Suppose you're interested calculating min and max streams within each continent, and each position.

    Now the output has one row for each combination of a continent and position.

    (Click down to see what the steps leading to this code might look like)

    Summarizing by continent and position

    (music_top200

  >> summarize(
      min_streams = _.streams.min(),
      max_streams = _.streams.max()
  )
)

    min_streams max_streams
    0 1470 12987027

    You might start by summarizing min and max streams across all the data.

    Summarizing by continent and position

    (music_top200
  >> filter(_.continent == "Oceania", _.position == 1)
  >> summarize(
      min_streams = _.streams.min(),
      max_streams = _.streams.max()
  )
)

    min_streams max_streams
    0 321272 1757343

    Then, you might add a filter, so your summarize is over one specific grouping (position 1 tracks in Oceania).

    Summarizing by continent and position

    (music_top200
  >> group_by(_.continent, _.position)
  >> summarize(
      min_streams = _.streams.min(),
      max_streams = _.streams.max()
  )
)

    continent position min_streams max_streams
    0 Africa 1 94422 94422
    1 Africa 2 74689 74689
    2 Africa 3 67552 67552
    ... ... ... ... ...
    997 Oceania 198 44570 225951
    998 Oceania 199 44364 225492
    999 Oceania 200 44291 225179

    1000 rows × 4 columns

    Finally, you might replace the filter with a group_by.

    Note that you might save this result as a variable and use it in a new pipe or visualization. For example, the new pipe might filter to keep where position is 1, so you can inspect min and max streams for the top tracks across continents.

    Let's practice!

    Exercise 1:

    Modify the code below so it calculates max popularity and average danceability for each artist.

    max_popularityavg_danceability
    0990.677937

    1 rows × 2 columns

    Make a scatterplot of the data.

    In the plot above, what strange thing is going on with the distribution of max popularity?

    possible answer

    There are many artists with a max popularity of 0!

    Exercise 2:

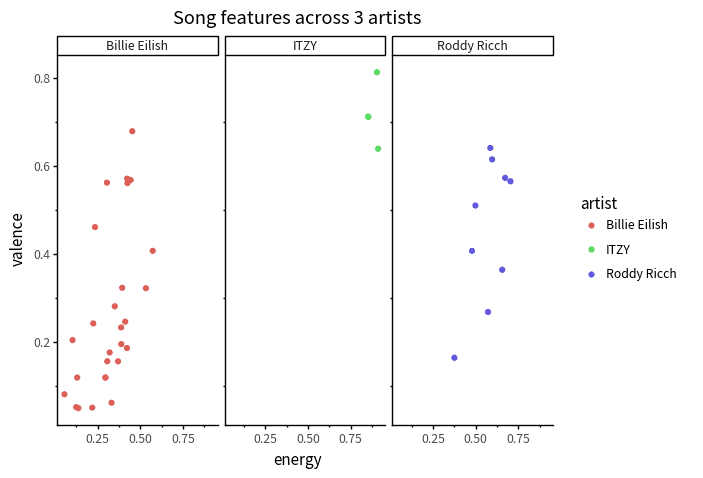
    In the last exercise of the facets chapter, you examined track features for three artists.

    We used a plot and intuition to judge who tended to have highest energy and valence tracks.

    png

    Now you should be able to answer the question more directly!

    Use a grouped summarize to calculate the mean energy and valence for each artist.

    Q: In this data, which artist has the lowest average energy, and what is its value?

    answerBillie Eilish, 0.321004

    Q: What about for lowest average valence?

    answerBillie Eilish, 0.266948
    prev pagenext page